随机排序算法简介

Posted on In Symbols count in article: 2.8k Reading time ≈ 3 mins.

前几天看了酷壳上的一篇文章如何测试洗牌程序，之后仔细看了Wikipedia对Fisher–Yates shuffle算法的介绍，这里简单的总结一下，基本是翻译Wikipedia。

Fisher and Yates’ original method

该算法最初是1938年由Ronald A. Fisher和Frank Yates在《Statistical tables for biological, agricultural and medical research》一书中描述，算法生成1-N个数的随机排列的过程如下：

  1. 原始数组中有数字1到N
  2. 设原始数组未被标记的数字个数为k，生成一个1到k之间的随机数
  3. 取出原始数组未被标记数字中的第k个，将其标记并插入到新的排列数组尾端。
  4. 重复过程2直到原始数组中没有未被标记的数字
  5. 过程3中生成的新数组就是一个对原始数组的随机排列

该算法可以理解为已知有n个元素，先从n个元素中任选一个，放入新空间的第一个位置，然后再从剩下的n-1个元素中任选一个，放入第二个位置，依此类推。算法在过程3查找未被标记的第k个数字有很多重复操作，导致算法效率并不高，总的时间复杂度为O(N^2 )，空间复杂度为O(N)。算法的python实现如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
from random import random

def FisherYateOldShullfe(items):
	ret = [None] * len(items)
	for i in reversed(range(0, len(items))):
		j = int(random() * (i+1))
		ret[i] = items[j]
		del items[j]
	return ret

if __name__ == '__main__':
	srclist = [n for n in range(10)]
	print FisherYateOldShullfe(srclist)

Modern version of the Fisher–Yates shuffle

改进版的Fisher–Yates shuffle算法是1964年Richard Durstenfeld在 Communications of the ACM volume 7, issue 7中首次提出，相比于原始Fisher-Yates shuffle最大的改进是不需要在步骤3中重复的数未被标记的数字，该算法不再将标记过的数字移动到一个新数组的尾端，而是将随机数选出的数字与排在最后位置的未标记数字进行交换。算法在python下的实现如下所示：

1
2
3
4
5
6
7
8
9
10
11
from random import random

def FisherYatesShuffle(items):
    for i in reversed(range(1, len(items))):
    	j = int(random() * (i+1))
	    items[i], items[j] = items[j], items[i]

if __name__ == '__main__':
	srclist = [n for n in range(10)]
	FisherYatesShuffle(srclist)
	print srclist

该算法同样可以理解成为这样的过程：从1到n个数字中依次随机抽取一个数字，并放到一个新序列的尾端（该算法通过互换数字实现），逐渐形成一个新的序列。计算一下概率：如果某个元素被放入第i（1≤i≤n）个位置，就必须是在前 i-1 次选取中都没有选到它，并且第 i 次恰好选中它。其概率为：

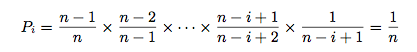
probability

算法中只有一个从1到N-1的循环，循环内操作为常数步，因而算法总的时间复杂度为O(N)，空间复杂度为O(1)。

Inside-out algorithm

Fisher-Yates shuffle是一种在原地交换的生成过程，即给定一个序列，算法在这个序列本身的存储空间进行操作。与这种in-place的方式不同，inside-out针对给定序列，会生成该序列随机排列的一个副本。这种方法有利于对长度较大的序列进行随机排列。 Inside-out算法的基本思想是从前向后扫描，依次增加i，每一步操作中将新数组位置i的数字更新为原始数组位置i的数字，然后在新数组中将位置i和随机选出的位置j（0≤j≤i）交换数字。算法亦可以理解为现将原始数组完全复制到新数组，然后新数组位置i(i from 1 to n-1)依次和随机位置j交换数字。算法的python实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from random import random

def insideout(source):
    ret = [None] * len(source)
    ret[0] = source[0]
    for i in range(1, len(source)):
        j = int(random() * (i+1))
        ret[i] = ret[j]
        ret[j] = source[i]
    return ret

if __name__ == '__main__':
	srclist = [n for n in range(10)]
	print insideout(srclist)

对于这个算法，我们分析可以出现多少种不同的排列数，从$i=1$开始，每一次交换都可以衍生出$(i+1)$倍的排列数，因而总的排列方案数如下图。在随机函数完全随机的情况下每一种排列都是等概率出现的，因而这种算法得到的是一个随机排序。它的时间复杂度和空间复杂度都是O(N)。

sum

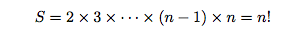
该算法有一个优点就是可以通过不断读取原始数组的下一个元素同时使新的排列数组长度加一，进而生成一个随机排列，即可以对长度未知的序列进行随机排列。实现的伪代码如下：

1
2
3
4
5
6
7
while source.moreDataAvailable
      j <- random integer with 0 <= j <= a.length
      if j = a.length
          a.append(source.next)
      else
          a.append(a[j])
          a[j] <- source.next

另一种想法

对n个元素的随机排序对应于这n个元素全排列中的一种，所以有这样一种方法求随机排序：求n个元素的随机排列，给定一个随机数k（1≤k≤n!），取出n!个全排列中的第k个即是一种随机排序。于是需要解决2个问题：一是在一个足够大的范围内求随机数；另外是实现一种是在n!个全排列中求第k个全排列的方法。第一个问题很古老，有人说随机数的最大范围决定于随即种子的大小，我有一种想法是对分段求随机数，比如需要求最大范围为N的随机数，那么可以对N进行M进制分解，分别求M进制下的每一位的随机数，最后合成一个大的随机数；而第二个问题就比较容易了，有很多全排列生成算法，通过“原排列”->“原中介数”->“新中介数”->“新排列”的过程，可以很方便的求出第k个全排列。

参考文章

洗牌程序，等概率随机排列数组（洗牌算法）